Complexity Analysis
Using software metrics like complexity analysis will guide you towards maintainable and testable pieces of code by reducing the complexity and splitting the code into smaller chunks.
Halstead Metrics
Calculation
First, we need to compute the following numbers, given the program:
- \(n_1\) = the number of distinct operators
- \(n_2\) = the number of distinct operands
- \(N_1\) = the total number of operators
- \(N_2\) = the total number of operands
From these numbers, five measures can be calculated:
- Program length: \(N = N_1 + N_2\)
- Program vocabulary: \(n = n_1 + n_2\)
- Volume: \(V = N \cdot log_2 n\)
- Difficulty: \(D = \frac{n_1}{2} \cdot \frac{N_2}{n_2}\)
- Effort: \(E = D \cdot V\)
The difficulty measure \(D\) is related to the difficulty of the program to write or understand, e.g. when doing code review.
The volume measure \(V\) describes the size of the implementation of an algorithm.
McCabe's Cyclomatic Complexity
Description
Cyclomatic complexity (or conditional complexity) is a software metric used to measure the complexity of a program. It directly measures the number of linearly independent paths through a program's source code.
Cyclomatic complexity is computed using the control flow graph of the program: the nodes of the graph correspond to indivisible groups of commands of a program, and a directed edge connects two nodes if the second command might be executed immediately after the first command. Cyclomatic complexity may also be applied to individual functions, modules, methods or classes within a program.
The cyclomatic complexity of a section of source code is the count of the number of linearly independent paths through the source code. For instance, if the source code contains no decision points, such as if statements or for loops, the complexity would be 1, since there is only a single path through the code. If the code has a single if statement containing a single condition there would be two paths through the code, one path where the if statement is evaluated as true and one path where the if statement is evaluated as false.
Calculation
Mathematically, the cyclomatic complexity of a structured program is defined with reference to a directed graph containing the basic blocks of the program, with an edge between two basic blocks if control may pass from the first to the second (the control flow graph of the program). The complexity is then defined as:
where
- \(M\) = cyclomatic complexity
- \(E\) = the number of edges of the graph
- \(N\) = the number of nodes of the graph
- \(P\) = the number of connected components.
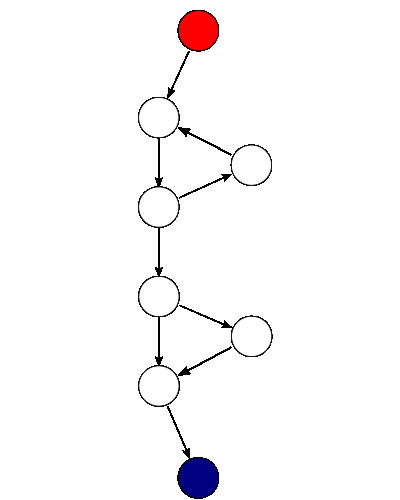
Take, for example, a control flow graph of a simple program. The program begins executing at the red node, then enters a loop (group of three nodes immediately below the red node). On exiting the loop, there is a conditional statement (group below the loop), and finally the program exits at the blue node. For this graph, \(E = 9\), \(N = 8\) and \(P = 1\), so the cyclomatic complexity of the program is \(3\).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | |
For a single program (or subroutine or method), P is always equal to 1. Cyclomatic complexity may, however, be applied to several such programs or subprograms at the same time (e.g., to all of the methods in a class), and in these cases P will be equal to the number of programs in question, as each subprogram will appear as a disconnected subset of the graph.
It can be shown that the cyclomatic complexity of any structured program with only one entrance point and one exit point is equal to the number of decision points (i.e., if statements or conditional loops) contained in that program plus one.
Cyclomatic complexity may be extended to a program with multiple exit points; in this case it is equal to:
Where
- \(\pi\) is the number of decision points in the program, and
- \(s\) is the number of exit points.